Triângulos: congruência e pontos notáveis
Congruência de figuras planas
Já trabalhamos com:
• Segmentos congruentes: têm mesma medida.
• Ângulos congruentes: têm mesma medida.
O que seriam figuras planas congruentes?
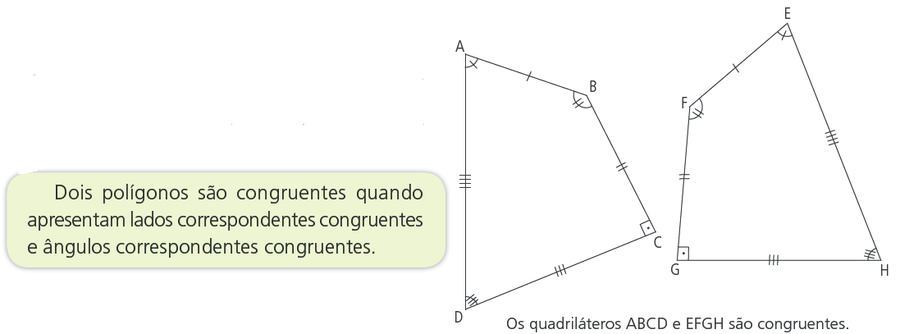
Se você copiar e recortar os quadriláteros ao lado, verá que eles se sobrepõem perfeitamente, ou seja, coincidem.
Duas figuras planas são congruentes se quando sobrepostas coincidem ponto a ponto.
Neste tópico trataremos da congruência de polígonos, em especial de triângulos. Com auxílio de régua e transferidor, meça os lados e os ângulos internos dos quadriláteros ABCD e EFGH. Anote os valores em seu caderno, em uma tabela.


A cada ângulo do quadrilátero ABCD corresponde um ângulo do quadrilátero EFGH, que é congruente a ele.
A cada lado do quadrilátero ABCD corresponde um lado do quadrilátero EFGH, que é congruente a ele.
Por exemplo, ao ângulo A corresponde o ângulo E e vice-versa. Usaremos “tracinhos” para identificar pares de lados e pares de ângulos correspondentes. Veja na figura ao lado.
Casos de congruência de triângulos
Triângulos são polígonos, portanto, para que dois triângulos sejam congruentes precisamos ter lados correspondentes congruentes e ângulos correspondentes congruentes.
Para decidirmos se dois triângulos são ou não congruentes, precisamos verificar 6 condições:
• 3 congruências entre lados correspondentes;
• 3 congruências entre ângulos correspondentes.
No entanto, os triângulos apresentam características que permitirão reduzir esse trabalho.
Caso LLL

Caso ALA

Caso LAL

Assista ao vídeo explicativo
sobre os casos de congruência entre triângulos
