Sistemas de equações - Vídeo e exercícios

Sistemas de Equações

Considere o seguinte problema:

Pipoca, em sua última partida, acertou x arremessos de 2 pontos e y arremessos de 3 pontos. Ele acertou 25 arremessos e marcou 55 pontos. Quantos arremessos de 3 pontos ele acertou?

Podemos traduzir essa situação através de duas equações, a saber:

x + y = 25 (total de arremessos certo)

2x + 3y = 55 (total de pontos obtidos)

Essas equações contém um sistema de equações.

Costuma-se indicar o sistema usando chave.

O par ordenado (20, 5), que torna ambas as sentenças verdadeiras, é chamado solução do sistema.Um sistema de duas equações com duas variáveis possui uma única solução.

Resolução de Sistemas

A resolução de um sistema de duas equações com duas variáveis consiste em determinar um par ordenado que torne verdadeiras, ao mesmo tempo, essas equações.

Estudaremos a seguir alguns métodos:

Método de substituição

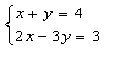
Solução

determinamos o valor de x na 1ª equação.

x = 4 - y

Substituímos esse valor na 2ª equação.

2 . (4 - y) -3y = 3

Resolvemos a equação formada.

8 - 2y -3y = 3

-5y = -5 => Multiplicamos por -1

5y = 5

y = 1

Substituímos o valor encontrado de y, em qualquer das equações, determinando x.

x + 1 = 4

x = 4 - 1

x = 3

A solução do sistema é o par ordenado (3, 1).

V = {(3, 1)}

Método da adição

Observe a solução de cada um dos sistemas a seguir, pelo método da adição.

Resolva o sistema abaixo:

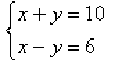
Solução

Adicionamos membros a membros as equações:

2x = 16

x = 8

Substituímos o valor encontrado de x, em qualquer das equações, determinado y:

8 + y = 10

y = 10 - 8

y = 2

A solução do sistema é o par ordenado (8, 2)

V = {(8, 2)}